Rakshak Adhikari

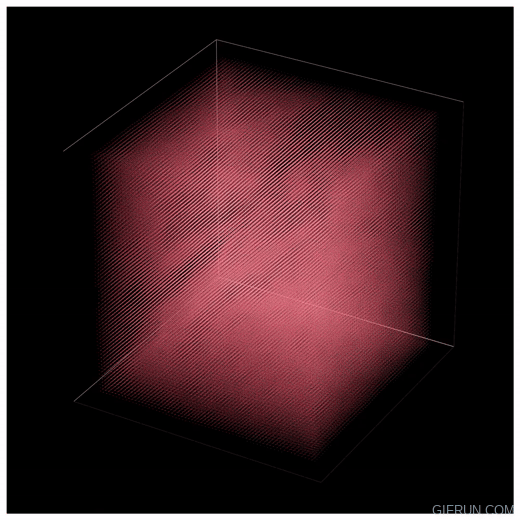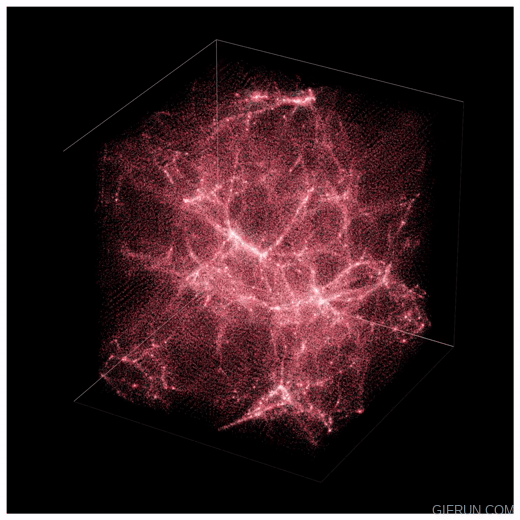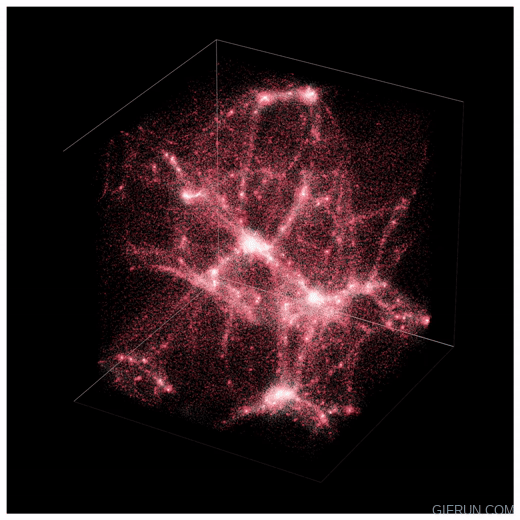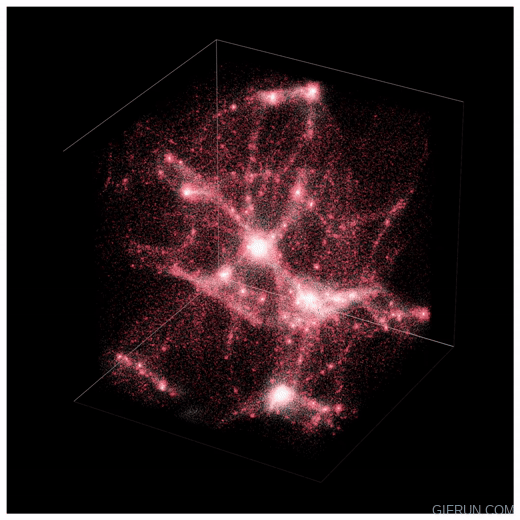Fig. Numerical Simulation showing structure formation. The red represents dark matter and the white regions represent star forming regions.

The Lambda-CDM or the Standard model of Cosmology mainly consists of three components: cosmological constant or Dark Energy (Lambda), CDM ( "cold" Dark Matter) and thirdly, Baryonic matter. Cold Dark matter simply means that the Dark matter particles are not relativistic and hence are slow enough to coalesce into halos to allow the formation of structure (galaxies, clusters of galaxies and so on).

Over the last several decades, cosmological simulations of galaxy formation have been critical in increasing our understanding of the structure formation in the Universe. Computer simulations are particularly necessary because structure formation is a manifestly non-linear phenomenon and these simulations are able to mimic a variety of physical processes over a wide range of time and length scales as galaxies and galaxy clusters evolve nonlinearly.

The cold dark matter (CDM) cosmological model has been very successful in explaining cosmic structure over a large range of redshifts but has experienced some problems at smaller scales. Particularly, it has encountered continuous challenges from studies of the Milky Way's dwarf galaxy satellites and the innermost regions of dark matter halos. These are generally termed as "small scale problems".

When compared to observations in the Milky Way (MW) environment, computer simulations of CDM consistently over-predict the number of small-mass (satellite) halos. This is called the missing satellites problem or the substructure problem. Another related problem is the so-called 'too-big-to-fail' (TBTF) problem. In numerical simulations, it was discovered that MW-type settings have a higher number of massive subhalos with denser halo centers than observed, and such massive subhalos should be able to host visible galaxies if they existed. In a way, the TBTF problem is the extension of the substructure problem at the higher mass end. Dark Matter-only ΛCDM simulations predict cuspy, ρ ∝ 1/r, profiles for halo densities. However, observations of Low Surface Brightness galaxies and dwarf spheroidals (which are thought to be DM dominated) have flat density profiles. This is known as the core-cusp problem.

A resolution could be found in the physics of various baryonic processes like supernova feedback, blackhole (AGN feedback) etc.

Another approach to resolve the small scale problems involves allowing dark matter to interact with itself via both elastic and inelastic scattering. In this model, Dark Matter particles exist in a superposition of two Mass eigenstate. This can be thought of as of fiducial case for a n-component dark-matter model. We can note that neutrons and axions, as well as some other Dark Matter candidates are expected to be flavor mixed. Each flavor is a particular combination of mass eigenstates and here, flavor determines the interaction, whereas mass determines the propagation. In non-relativistic regimes, the different Mass eigenstates move at different speeds and can effectively be treated as two different particles. The free parameter in this theory is the interaction cross section, it's velocity dependence between the mass eigenstates. The 2CDM model is distinct from the SIDM( Self-Interacting Dark Matter) model in that it allows for inelastic scattering i.e. Particle conversion from heavy to light and vice versa. While Self-Interacting Dark Matter can solve the substructure problem, it cannot solve the TBTF as well as the core-cusp problem. However, 2cdm model has the potential to solve all the small-scale problems simultaneously.

For an introduction to the 2CDM model, see the talk by professor Medvedev at the University of Kansas.

To learn more about the Arepo code used in the simulations, check out the following link.